Discussion :: Alligation or Mixture
-
A vessel is filled with liquid, 3 parts of which are water and 5 parts syrup. How much of the mixture must be drawn off and replaced with water so that the mixture may be half water and half syrup?
Answer : Option C
Explanation :
Suppose the vessel initially contains 8 litres of liquid.
Let x litres of this liquid be replaced with water.
Quantity of water in new mixture =[ 3- \(\frac { 3X } { 8 } \) +x]litres
Quantity of syrup in new mixture =[5 - \(\frac { 5X } { 8 } \)]litres
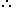 [3- \(\frac { 3X } { 8 } \)+x] =[ 5-\(\frac { 5X } { 8 } \)]
[3- \(\frac { 3X } { 8 } \)+x] =[ 5-\(\frac { 5X } { 8 } \)]
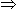 5x + 24 = 40 - 5x
5x + 24 = 40 - 5x
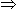 10x = 16
10x = 16
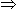 x =\(\frac {8 } {5 } \)
x =\(\frac {8 } {5 } \)
So, part of the mixture replaced = [\(\frac {8 } {5 } \)x \(\frac {1 } {8 } \)]=\(\frac {1 } {5 } \)
Be The First To Comment


 Whatsapp
Whatsapp
 Facebook
Facebook

