Pipes and Cistern - Arithmetic Aptitude Questions and Answers

Home / Arithmetic Aptitude / Pipes and Cistern :: Discussion

Discussion :: Pipes and Cistern

Two pipes A and B can fill a tank in 15 minutes and 20 minutes respectively. Both the pipes are opened together but after 4 minutes, pipe A is turned off. What is the total time required to fill the tank?

10 min. 20 sec.

11 min. 45 sec.

12 min. 30 sec.

14 min. 40 sec.

View Answer

Workspace

Whatsapp
Facebook
Copy
Copy Text
Copy
Copy URL

View Answer

Answer : Option D

Explanation :

Part filled in 4 minutes =4 [ $\frac { 1 } { 15 }$ + $\frac { 1 } { 20 }$ ] = $\frac { 7 } { 15}$

Remaining part =[1- $\frac { 7 } { 15}$ ]= $\frac { 8 } { 15}$

Part filled by B in 1 minute = $\frac { 1 } { 20 }$

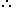$\frac { 1 } { 20 }$ : $\frac { 8 } { 15}$ ::1:x

x =[ $\frac { 8 } { 15}$ x1 x20]=10 $\frac {2 } { 3 }$ min = 10 min. 40 sec.

The tank will be full in (4 min. + 10 min. + 40 sec.) = 14 min. 40 sec.

Write your comments here:

Be The First To Comment

Comments

Name