Discussion :: Problems on Trains
-
A train travelling at 48 kmph completely crosses another train having half its length and travelling in opposite direction at 42 kmph, in 12 seconds. It also passes a railway platform in 45 seconds. The length of the platform is
Whatsapp
Facebook
Answer : Option A
Explanation :
Let the length of the first train be x metres.
Then, the length of the second train is \( (\frac { X} { 2 } ) metres\)
Relative speed = (48 + 42) kmph = \((90\times\frac{5}{18})m/sec = 25m/sec\)
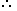\(\frac{(X +\frac{X}{2})}{25}=12 \) or \((\frac { 3X } { 2 } ) =300\) or X=200
Let the length of platform be y metres.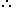
Length of first train = 200 m.
Speed of the first train = \((48\times\frac{5}{18})m/sec\) = \( (\frac { 40 } { 3 } ) m/sec\)
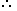\(((200+y)\times\frac{3}{40})\) =45
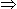600 + 3y = 1800
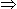y = 400 m.
Be The First To Comment