Answer : Option A

Explanation :

 I.    (10 x 6) men can complete the work in 1 day.

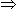 1 man's 1 day's work =$\frac { 1 } { 60 }$

II  .$[10*\frac { 24} {7 } ]$men +$[10*\frac { 24} {7 } ]$women can complete the work in 1 day

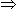$( \frac {2 40 } { 7} )$men's 1 day work +$( \frac {2 40 } { 7} )$women's 1 day work = 1

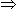$[ \frac {2 40 } { 7}$$*\frac {1} {60 } ]$+$( \frac {2 40 } { 7} )$women's 1 day's work = 1

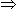$( \frac {2 40 } { 7} )$women's 1 day's work =[1-$\frac { 4 } { 7 }$]=$\frac {3 } { 7 }$

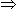 10 women's 1 day's work =[$\frac {3 } { 7 } *$$\frac {7 } { 240 } *10]$=$\frac { 1 } { 8 }$

So, 10 women can finish the work in 8 days.

III. (10 men's work for 3 days) + (10 women's work for 4 days) = 1

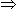       (10 x 3) men's 1 day's work + (10 x 4) women's 1 day's work = 1

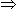       30 men's 1 day's work + 40 women's 1 day's work = 1

      Thus, I and III will give us the answer.     

      And, II and III will give us the answer