Discussion :: Time and Work
-
In how many days can 10 women finish a work?
I.10 men can complete the work in 6 days.
II.10 men and 10 women together can complete the work in 3\(\frac { 3 } { 7 } \)days.
III.If 10 men work for 3 days and thereafter 10 women replace them, the remaining work in completed in 4 days.
Answer : Option A
Explanation :
I. (10 x 6) men can complete the work in 1 day.
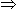 1 man's 1 day's work = \(\frac { 1 } { 60}\)
1 man's 1 day's work = \(\frac { 1 } { 60}\)
II. \( [10*\frac { 24 } { 7 } ]\)men+\( [10*\frac { 24 } { 7 } ]\) women can complete the work in 1 day.
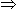 \([\frac {240 } { 7} ]\) men's 1 day work +\([\frac {240 } { 7} ]\) women's 1 day work = 1
\([\frac {240 } { 7} ]\) men's 1 day work +\([\frac {240 } { 7} ]\) women's 1 day work = 1
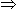 [\(\frac {240 } { 7}\) x \(\frac {1 } { 60} \)] +\([\frac {240 } { 7} ]\) women's 1 day's work = 1
[\(\frac {240 } { 7}\) x \(\frac {1 } { 60} \)] +\([\frac {240 } { 7} ]\) women's 1 day's work = 1
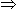 \([\frac {240 } { 7} ]\)women's 1 day's work =[1-\( \frac { 4 } { 7 } \)] =\(\frac { 3 } { 7 } \)
\([\frac {240 } { 7} ]\)women's 1 day's work =[1-\( \frac { 4 } { 7 } \)] =\(\frac { 3 } { 7 } \)
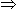 10 women's 1 day's work =[ \(\frac { 3 } { 7 } \)x\( \frac {7 } { 240 }\)x 10] =\(\frac { 1} { 8 } \) 10 women's 1 day's work =[ \(\frac { 3 } { 7 } \)x\( \frac {7 } { 240 }\)x 10] =\(\frac { 1} { 8 } \) |
So, 10 women can finish the work in 8 days.
III. (10 men's work for 3 days) + (10 women's work for 4 days) = 1
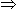 (10 x 3) men's 1 day's work + (10 x 4) women's 1 day's work = 1
(10 x 3) men's 1 day's work + (10 x 4) women's 1 day's work = 1
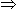 30 men's 1 day's work + 40 women's 1 day's work = 1
30 men's 1 day's work + 40 women's 1 day's work = 1
Thus, I and III will give us the answer.
And, II and III will give us the answer.
 Correct answer is (A)
Correct answer is (A)
Be The First To Comment


 Whatsapp
Whatsapp
 Facebook
Facebook

