Discussion :: Exam Questions Paper
-
Consider a stable and causal system with impulse response h(t) and system function H(S). Suppose H(S) is rational, contains a pole at S = - 2, and does not have a zero at the origin. The location of all other poles and zero is unknown for each of the following statements. Let us determine whether statement is true or false.
- f[h(t) e-3t] converges
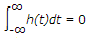
- h(t) has finite duration
- H(s) = H(- s)
|
A.
1 - True, 2 - False, 3 - True, 4 - False
|
|
B.
1 - False, 2 - False, 3 - False, 4 - True
|
|
C.
1 - False, 2 - False, 3 - False, 4 - False
|
|
D.
1 - True, 2 - can't say, 3 - True, 4 - can't say
|
Whatsapp
Facebook
Answer : Option C
Explanation :
Statement 1 is false, since f{h(t)e3t} corresponds to the value of the Laplace transform of h(t) at s = 3.
If this converges, it implies that s = - 3 is in the ROC.
A casual and stable system must always have its ROC to the right of all its poles. However, s = - 3 is not to the right of the pole at s = - 2.
Statement 2 is false, because it is equivalent to stating that H(0) = 0. This contradicts the fact that H(s) does not have a zero at the origin.
Statement 3 is false. If h(t) is of finite duration, then if its Laplace transform has any points in its ROC, ROC must be the entire s-plane.
However, this is not consistent with H(s) having a pole at s = - 2.
Statement 4 is false. If it were true, then H(s) has a pole at s = - 2, it must also have a pole at s = 2.
This is inconsistent with the fact that all the poles of a causal and stable system must be in the left half of the s-plane.
Be The First To Comment