Discussion :: Exam Questions Paper
-
The fourier transform of the half cosine pulse as shown below is __________
|
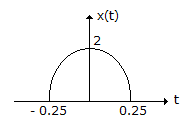
A.
0.5 {sin [0.5(f - 1)] + sin [0.5 (f + 1)]}
|
|
B.
0.25 [sin c[0.25 (f - 2)1 + sin c[0.25(f + 2)]]
|
|
C.
0.5 {sin c [0.5 (f - 1)] + sin c [0.5 (f + 1)]}
|
|
D.
sin c(f - 0.5) + sin c (f + 0.5)
|
Whatsapp
Facebook
Answer : Option C
Explanation :
The given signal can be expressed as multiplication of x1(t) and x2(t) as shown below, where A = 2, T/2 = 0.25 ⇒ T = 0.5
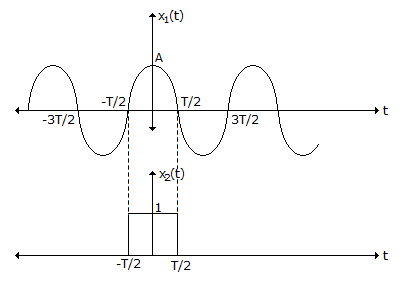
∴ x(t) = x1(t) x x2(t)
⇒ X(f) = X1(f) * X2(f)
Now X1(f) =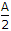 
[δ(f - f0) + δ(f + f0)]
where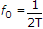 
and X2(f) = T . sin c[fT]
⇒ X(f) = 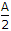[δ(f - f0) + δ(f + f0)]
*T. sinc(fT)
= 
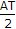[sinc[T(f - f0)] + sinc [T(f + f0)]]
Now, A = 2, T = 0.5
and 
⇒ X(f) = 0.5[sin c(0.5(f - 1)) + sinc(0.5(f + 1))].
Be The First To Comment