Discussion :: Signals and Systems
-
If f1 (t) and f2 (f) are two functions of time and a and b are constants, then
|
A.
L [af1(t) + bf2(t)] = aF1(s) + bF2(s)
|
|
B.
L [af1(t) + bf2(t)] = aF1(s) - bF2(s)
|
|
C.
L [af1(t) + bf2(t)] =[aF1(s)]/[bF2(s]
|
|
D.
None of the above
|
Whatsapp
Facebook
Answer : Option A
Explanation :
£f(t) =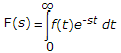 
£-1F(s) = f(t)
£[a f1(t) + bf2(t)] = aF1(s) + bF2(s)
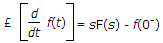
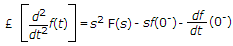
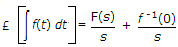
where 
£[f(t - T)] = e-sT F(s)
£[e-at f(t)] = F(s + a)
Initial value theorem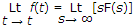 
Final value theroem 
Convolution Integral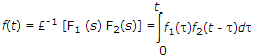 
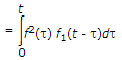
where t is dummy variable for t.
Be The First To Comment