GATE 2017-2018 :: GATE Mathematics
- Suppose the random variable U has uniform distribution on [0,1] and X =−2logU. The density of X is
- Let f be an entire function on ℂ such that |f(z)| ≤ 100 log|z| for each z with |z| ≥ 2. If F(i) = 2i then f(1)
-
Suppose X is a random variable with P(X = k) = (1 - p)kp for k ∈ {0,1,2,..} and some p ∈ (0,1). For the hypothesis testing problem H0:p = 1/2 H1:p ≠1/2consider the test "Reject H0 if X ≤ A or if X ≥ B", where A < B are given positive integers. The type-I error of this test is
- Let G be a group of order 231. The number of elements of order 11 in G is ______
- Let f:â„2→â„2 be defined by f(x,y) = (ex+y, ex-y). The area of the image of the region {(x,y) ∈â„2:0 < x,y < 1} under the mapping f is
- Which of the following is a field?
- Let x0 = 0. Define xn+1 = cos xn for every n≥0. Then
-
Let C be the contour |z| = 2 oriented in the anti-clockwise direction. The value of the integral
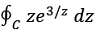is
.
.
.
.
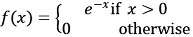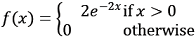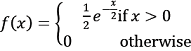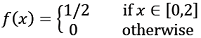Whatsapp
Facebook
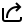
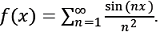Then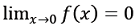 
.
.
.
.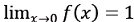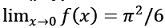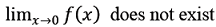