Civil Engineering :: Theory of Structures
-
The forces acting normally on the cross section of a bar shown in the given figure

-
If the normal stresses due to longitudinal and transverse loads on a bar are σ1 and σ2 respectively, the tangential component of the stress on an inclined plane through θ°, the longitudinal load is
-
The ratio of the section modulus of a square section of side B and that of a circular section of diameter D, is
-
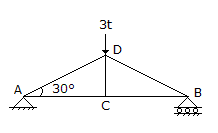
The force in BC of the truss shown in the given figure, is
-
The equivalent length of a column of length L, having one end fixed and other end hinged, is
-
At any point of a beam, the section modulus may be obtained by dividing the moment of inertia of the section by
-
For calculating the permissible stress \(\frac { \sigma y } { 1+a(1/r)^2 } \) is the emprical formula, known as
-
The maximum height of a masonry dam of a triangular section whose base width is b and specific gravity s, is
-
The load on a spring per unit deflection, is called
-
In a shaft, the shear stress is not directly proportional to


 Whatsapp
Whatsapp
 Facebook
Facebook