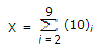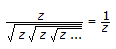ECE :: Exam Questions Paper
-
A system described by the following differential equation
 is initially at rest. For input x(t) - 2u(t), the output y(t) is :
is initially at rest. For input x(t) - 2u(t), the output y(t) is : -
A transmission line terminates in two branches, each of length λ/4, as shown. The branches are terminated by 50Ω loads. The lines are lossless and have the characteristics impedances shown. Determine the impedance Z1 as seen by the source

-
The Nyquist plot of
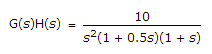
-
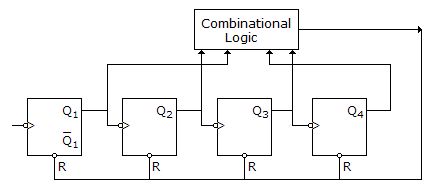
The counter shown in figure is built using 4 negative edge triggered toggle FFs. The FFs can be set synchronously when R = 0. The combinational logic required to realize a modulo 13 counter is
-
Consider the following statements a half adder.
- As a half subtractor also
- has two outputs CH = x x y and Sn = x ⊕ y for two inputs x and y
- has two outputs CH = x + y and SH = x ⊕ y for two inputs x and y
- is a combinational circuit
-
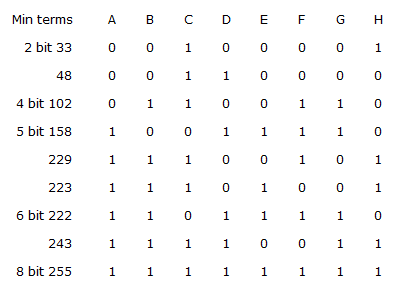
The expression given is F(A, B, C, D, E, F, G, H) = Σ(33, 48, 102, 158, 222, 229, 233, 243, 255); then the __________ and __________ minterms are grouped together into dual and variable __________ is reduced using the dual
-
If for certain x(t), the Fourier transform is:
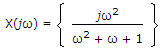
Then for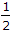 x(2t) the Fourier transform will be:
x(2t) the Fourier transform will be: -
The Z-inverse of the given Z-transform is __________
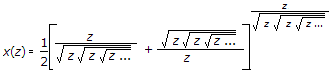
|
A.
will start from (ω = ∞) in the first quadrant and will terminate (ω = 0) in the second quadrant
|
|
B.
will start from (ω = ∞) in the fourth quadrant and will terminate (ω = 0) in the second quadrant
|
|
C.
will start form (ω = ∞) in the second quadrant and will terminate (ω = 0) in the fourth quadrant
|
|
D.
will start from (ω = ∞) in the first quadrant and will terminate (ω = 0) in the fourth quadrant
|


 Whatsapp
Whatsapp
 Facebook
Facebook


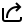
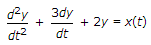
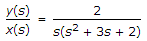
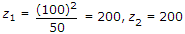

 .
.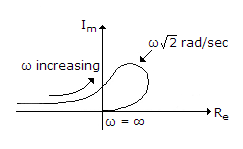


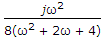
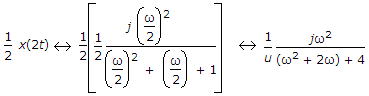 .
.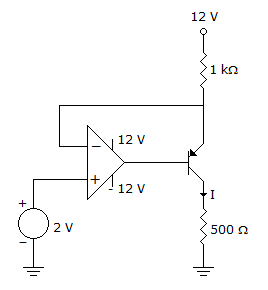
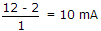
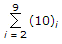 the value of x is
the value of x is