Mechanical Engineering :: Engineering Mechanics
-
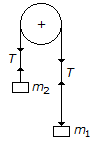
If the masses of both the bodies, as shown in the below figure, are doubled, then the acceleration in the string will be
-
The loss of kinetic energy during inelastic impact, is given by(where m1 = Mass of the first body,m2 = Mass of the second body, and u1 and u2 = Velocities of the first and second bodies respectively.)
-
The centre of gravity of a hemisphere lies at a distance of 3r / 8 from its base measured along the vertical radius
-
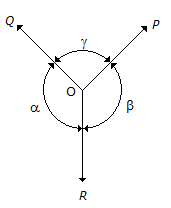
The above figure shows the three coplaner forces P, Q and R acting at a point O. If these forces are in equilibrium, then -
Moment of inertia of a rectangular section having width (b) and depth (d) about an axis passing through its C.G. and parallel to the depth (d), is
|
A.
\(\frac { P } { sin\beta } = \frac { Q } { sin\alpha } = \frac { R } { sin\gamma}\) |
|
B.
\(\frac { P } { sin\alpha } = \frac { Q } { sin\beta } = \frac { R } { sin\gamma}\) |
|
C.
\(\frac { P } { sin\gamma} = \frac { Q } { sin\alpha } = \frac { R } { sin\beta}\) |
|
D.
\(\frac { P } { sin\alpha } = \frac { Q } { sin\gamma} = \frac { R } { sin\beta}\) |


 Whatsapp
Whatsapp
 Facebook
Facebook