Arithmetic Aptitude :: Surds and Indices
-
If\( [\frac { a } { b }]^X-1\)=\([\frac { b} { a }] ^X-3\), then the value of x is
-
Given that 100.48 = x, 100.70 = y and xz = y2, then the value of z is close to:
-
\( \frac { 1 } {1+X(b-a)+X(c-a) } \)+\(\frac { 1 } { 1+X(a-b)+X(c-b) }+ \)\(\frac { 1 } {1+X(b-c)+X(a-c)}=?\)


 Whatsapp
Whatsapp
 Facebook
Facebook


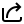
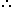 3.5 + x = 8
3.5 + x = 8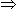 x = (8 - 3.5)
x = (8 - 3.5) 10(0.48z) = 10(2 x 0.70) = 101.40
10(0.48z) = 10(2 x 0.70) = 101.40