Surds and Indices - Arithmetic Aptitude Questions and Answers

Whatsapp
Facebook
Copy
Copy Text
Copy
Copy URL
Share as Image
As Image

Answer : Option C

Explanation :

Given Expression= $\frac { (243)^n/5*362n+1} { 9^n*3^n-1 }$

= $\frac {(3)^((n/5)*3^2n+1} { (3^2)^n*3^n-1}$

= $\frac {(3)^((n/5)*3^2n+1} { (3^2n*3^n-1)}$

= $\frac { 3^n*3^2n+1} {3^2n *3^n-1}$

= $\frac { 3(n+2n+1} {3(2n+n-1 }$

= $\frac {3^3n+1} { 3^3n-1 }$

= 3^{(3n + 1 - 3n + 1)} = 3² = 9.

$\frac { 1 } { 1+a^(n-m) } +$ $\frac { 1 } { 1+a^(m-n) }=?$

$\frac { 1 } { 2 }$

a^m + n

Whatsapp
Facebook
Copy
Copy Text
Copy
Copy URL
Share as Image
As Image

Answer : Option C

Explanation :

$\frac { 1 } { 1+a^(n-m) } +$ $\frac { 1 } { 1+a^(m-n) }=$ $\frac { 1 } {[1+ a^n/a^m]}+$ $\frac { 1 } {[1+ a^m/a^n]}$

= $\frac {a^m } { (a^m+a^n)}$ + $\frac {a^n } { (a^m+a^n)}$

= $\frac { (a^m+a^n) } { (a^m+a^n)}$

If m and n are whole numbers such that mⁿ = 121, the value of (m - 1)^{n + 1} is:

121

1000

Whatsapp
Facebook
Copy
Copy Text
Copy
Copy URL
Share as Image
As Image

$[\frac { X^b } {X^c } ]^(b+c-a)$ . $[\frac { X^c } {X^a} ]^(c+a-b)$ $[\frac { X^a} {X^b} ]^(a+b-c)=?$

x^abc

x^{ab + bc + ca}

x^{a + b + c}

Whatsapp
Facebook
Copy
Copy Text
Copy
Copy URL
Share as Image
As Image

If x = 3 +2 $\sqrt{2}$ , then the value of	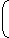	$\sqrt{X}$	-	1	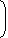	is:
				$\sqrt{X}$

$2\sqrt{2}$

3 $\sqrt{3}$

Whatsapp
Facebook
Copy
Copy Text
Copy
Copy URL
Share as Image
As Image