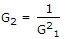ECE :: Automatic Control Systems
-
For a second order system with 0 < ξ < 1, the angle which poles make with negative real axis is
-
Consider the following statements
- The effect of feedback is to reduce system error
- Feedback increases the system gain at one frequency but reduces the system gain as another frequency
- Feedback can cause an originally stable system to become unstable
-
M circles are symmetrical with respect to
-
A lag compensator
-
Assertion (A): An on off controller gives rise to oscillation of the output between two limits.
Reason (R): Location of a pair of poles on jω axis gives rise to self sustained oscillations in the output.
-
Consider the following statements about transport-lag
- It is of non-minimum phase behaviour
- It normally exists in thermal, hydraulic and pneumatic systems
- It has an excessive phase lag with no attenuation at high frequency
-
Consider the following statements:
- If any root of characteristic equation has a positive real part the impulse response is unbounded and system is unstable.
- If all the roots of a characteristic equation have negative real parts, the impulse response decays to zero.
- If one or more non-repeated roots of characteristic equation are on jω axis impulse response is bounded but the system is unstable.
-
If block diagrams of the given figure (a) and (b) are to be equivalent, then
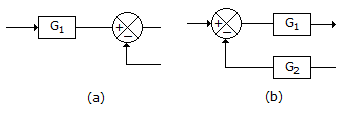
-
In root locus analysis the breakaway and break in points


 Whatsapp
Whatsapp
 Facebook
Facebook